Persamaan Lingkaran Matematika

Matematika - Berikut posting tentang Persamaan Lingkaran Matematika. Tapi, ini cuma ringkasan materinya aja-_- untuk latihan dan contoh soal menyusul ya.
Persamaan Lingkaran adalah tempat kedudukan titik-titik (x,y) yang
berjarak sama terhadap satu titik tertentu.
Mencari jarak antara 2 titik A (x1,y1) dan B
(x2,y2):
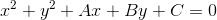
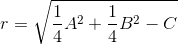
Kedudukan Garis Terhadap Lingkaran
Untuk mengetahui kedudukan/ posisi sebuah garis terhadap
lingkaran, substitusikan garis terhadap lingkaran sehingga didapatkan bentuk ax2+bx+c=0.
Dengan
diskriminannya:
Persamaan Garis Singgung Lingkaran
Persamaan garis
singgung untuk suatu titik (x1,y1) yang terletak pada
lingkaran
- Jika persamaan lingkaran x^2 + y^2 = r^2, maka persamaan garis singgungnya adalah :x1.x + y1.y = r^2
- Jika persamaan lingkaran (x-xp)^2 + (y-yp)^2 = r^2, maka persamaan garis singgungnya: (x1-xp)(x-xp) + (y1-yp)(y-yp) = r^2
- Jika persamaan lingkaran berbentuk x^2 + y^2 + Ax + By + C = 0, maka persamaan garis singgungnya: x1.x + y1.y + 1/2A(x+x1) + 1/2B(y+y1) + C = 0
Persamaan garis singgung dengan gradien m:
atau dengan
Sekian postingan Lingkaran Matematika semoga bermanfaat..
Terimakasih udah mampir di blog ini

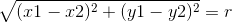
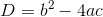
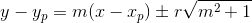
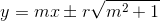










0 comments:
Post a Comment